Watch on Github

I’ve been learning a bit about deep neural networks on Udacity’s Deep Learning course (which is mostly a Tensorflow tutorial). The course uses notMNIST as a basic example to show how to train simple deep neural networks and let you achieve with relative ease an impressive 96% precision.

In my way to the top of Mount Stupid, I wanted to get a better sense of what the NN is doing, so I took the examples of the first two chapters and modified it to test an idea: create some simple models, generate some training and test data sets from them, and see how the deep network performs and how different parameters affect the result.

The models I’m using are two dimension (x,y) real values from [-1,1] that can be classified in two classes, either 0 or 1, inside or outside, true or false. The classification is a function that makes increasingly hard to classify the samples:

• positivos: A trivial classification – if x>0 class=1 else class=0
  
• linear: if y>x class=1 else class=0
  
• circle: if (x,y) is inside a circle of radius=r then class=1 else class=0
  
• ring: if (x,y) is inside a circle of radius=r but outside a concentric circle or radius=r/2 then class=1 else class=0
  
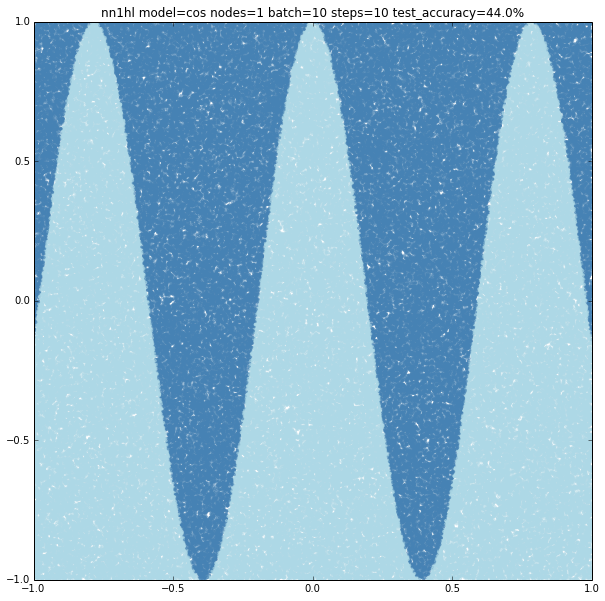
• cos: if (x,y) is above a cosine with frequency=r then class=1 else class=0
  
• polar: if (x,y) is below a cosine of frequency r in polar coordinates (inside a “rose of n-petals”) then class = 1 else class = 0
  

The plots shown above are generated from the training sets by setting positive samples as dark blue and negative samples as light blue.

Two neural networks are defined on the code, with a single hidden layer and with two hidden layers. Several parameters may be adjusted for each run:

• model function to use
• number or nodes of each layer,
• batch size and number of steps for the stochastic gradient descent of the training phase,
• beta for regularisation,
• standard deviation for the initialisation of the variables,
• and learning rate decay for the second NN

Other parameters are treated as globals such as the size of the training, validation and test sets.  When the NN function is called the network is trained and tested, and the predictions are added to the plot marking them on gray if the prediction was correct and on red if the prediction as incorrect in order to see where the classifier is missing it.

You can call the NN function varying the parameters to test what happens. It’s also included some iterative code to test many variants and generate a *lot* of plots. Check the code and comment what you find.

Here are some interesting results I’ve got:

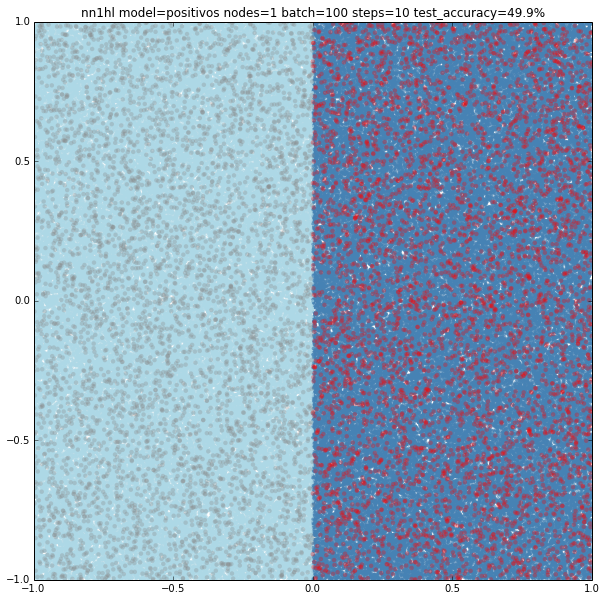
Trivial model with a single hidden node and few training data

As expected, the model is too simple to really learn anything: it’s basically classifying everything as negative and thus gets a accuracy of 49.9%

 

Trivial model with a single hidden node with more training data

By increasing the size of the batches and steps for the stochastic gradient descent even a single node on the hidden layer yields good results: 99.6% accuracy

 

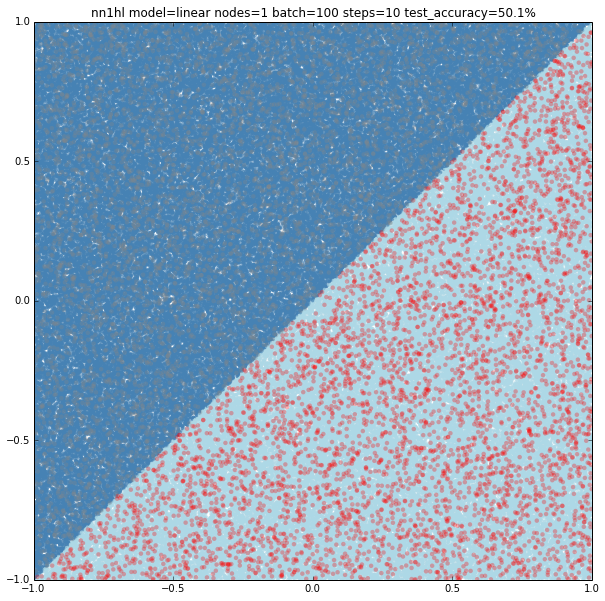
Linear model with a single hidden node and few training data

Of course few training data does anything good for a slightly more complex model: 50.1% accuracy.

 

Linear model with a single hidden node with more training data

Again the classifier performs way better: 99.9%

 

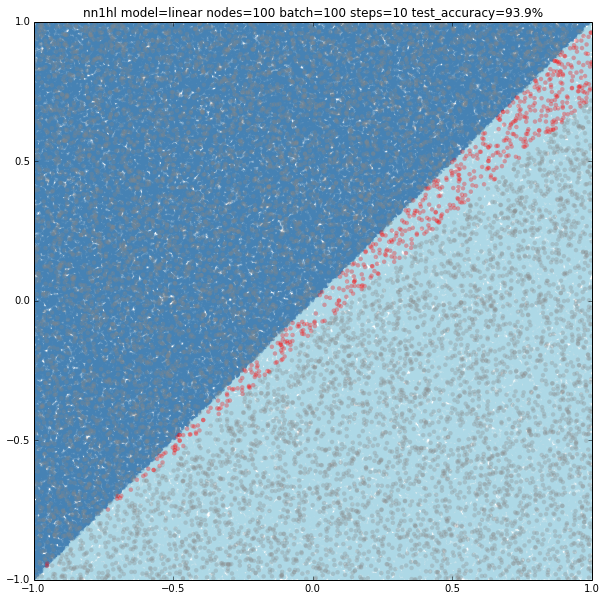
Linear model with a 100 hidden nodes with few training data

Can hidden nodes compensate for few training samples? 100 nodes, batch of 100 and 10 steps does certainly better at 93.9% accuracy and an interesting plot with linear classification on a wrong (but close) slope.

 

Linear model with a 1000 hidden nodes with few training data

What about 1000 hidden nodes and same parameters as before? It certainly gets you closer but not still on it: 98% accuracy. Watching the slope, one can think it may be overfitting.

 

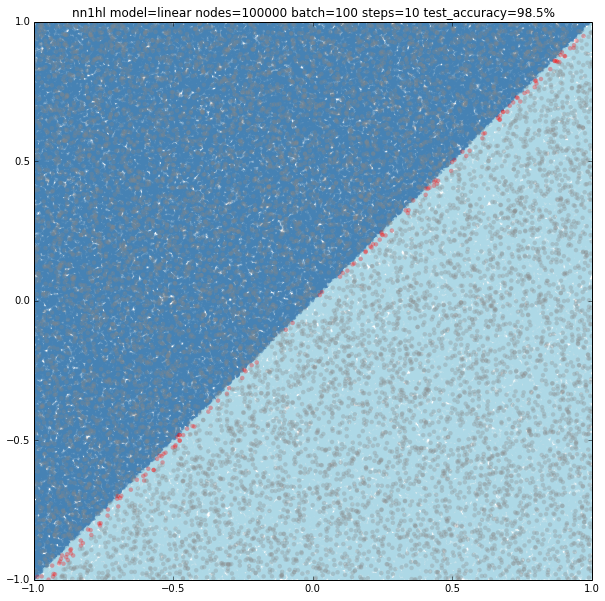
Linear model with lots of hidden nodes and few training data

First tried 10,000 hidden nodes (got 98.9%) and then 100,000 nodes (shown below) and accuracy jumped back to 98.5%, clearly overfitting. For this case, a wider network behaves better but just to a certain point.

 

Circle with a previously good classifier

Training the classifier that previously behaved well with the circular model shows clearly it needs more data or nodes.

 

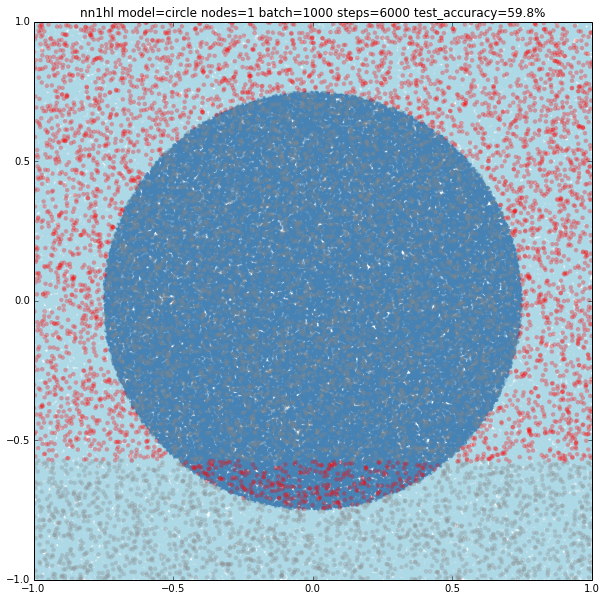
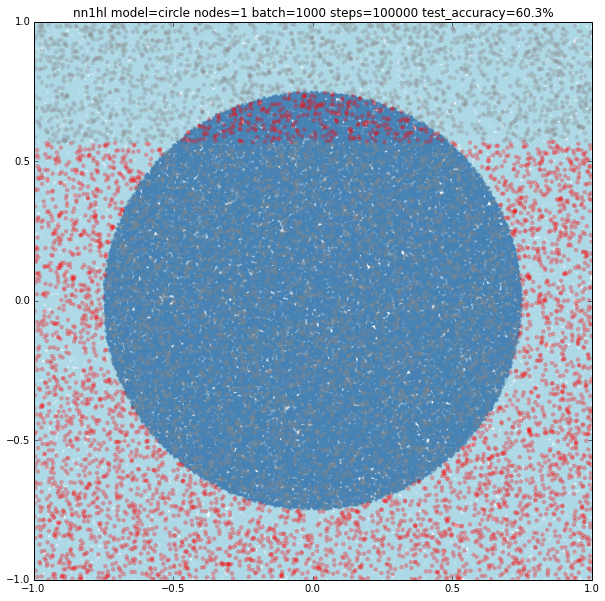
Circle with a single node

Turns out that it seems a single node can’t capture the complexity of the model. Varying the training parameters looks that the NN is always trying to adjust a linear classifier.

 

Circle with a many nodes and different training sizes

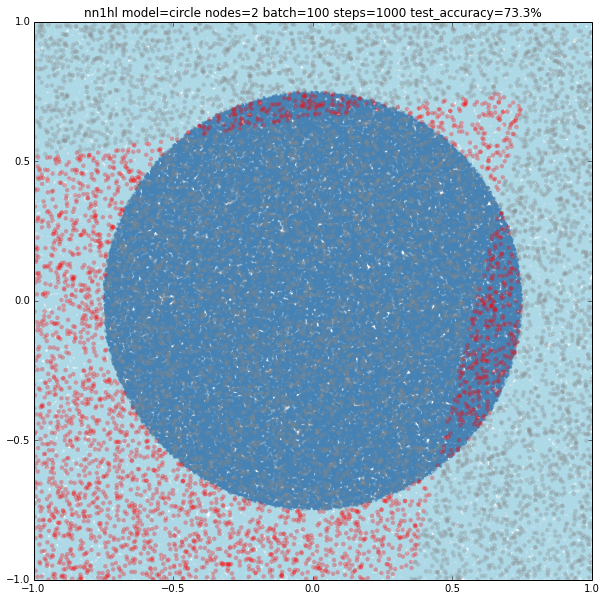
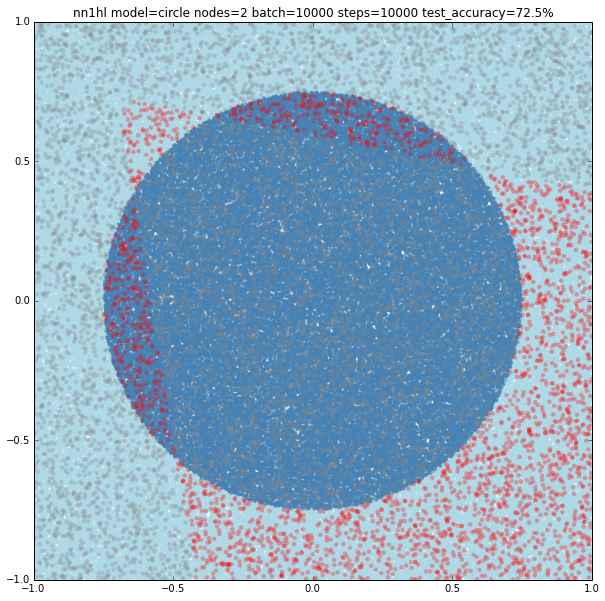
Two nodes

With two nodes the model looks like fitting two linear classifiers. Even varying the training parameters results are similar, except in some cases with more training data that looks like the last examples of single node (maybe overfitting?)

Three and more nodes

Using three nodes things become interesting. For a batch size of 100 and 1000 steps the NN gives a pretty good approximation to the circle and goes beyond adjusting 3 linear classifiers. Something similar happens varying the training parameters.

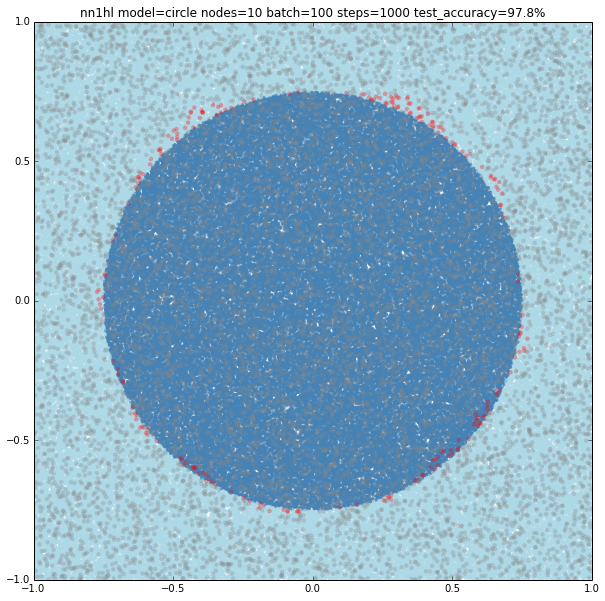
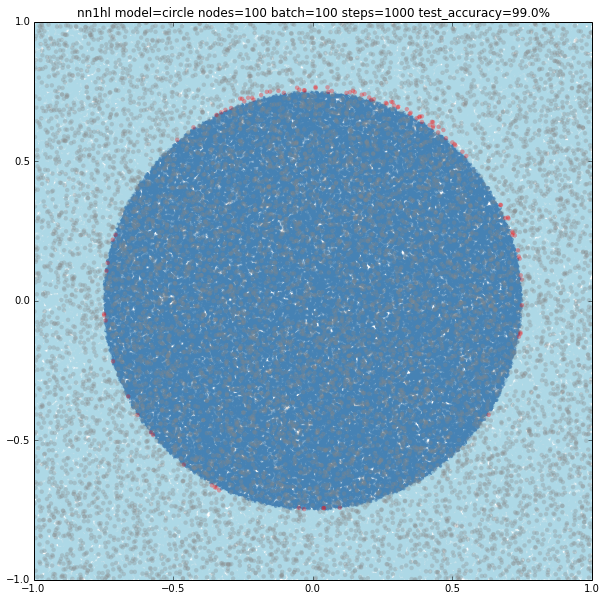
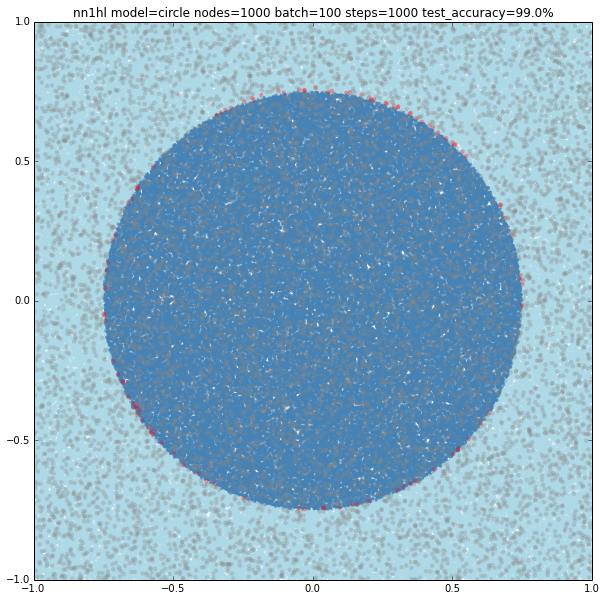
Increasing the number of nodes increases the precision and the visual adjustment to the circle. Check for 10 (97.8%), 100 (99%) and seems to stop at some point 1000 (99%)
 

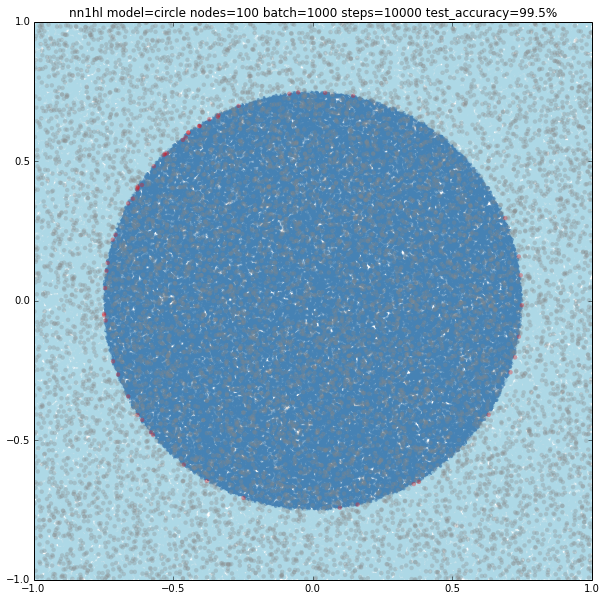
Finally increasing the training parameters on the best classifier gives us a nice 99.5% accuracy, but not sure if it’s overfitting

 

The Ring

For the ring I started testing one of the best performers on the circle: 100 nodes, batch size of 100 and 1000 steps. Somehow expected, it tried to adjust to a single circle and missed the inner one.

Increasing the training parameters gave an interesting and unexpected result:

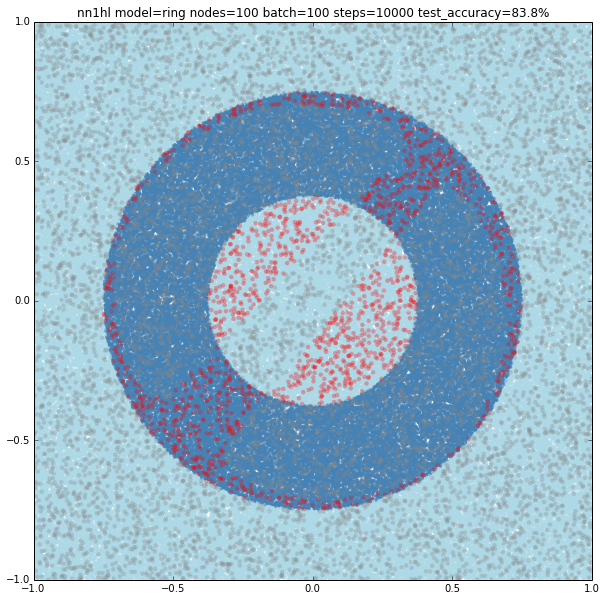
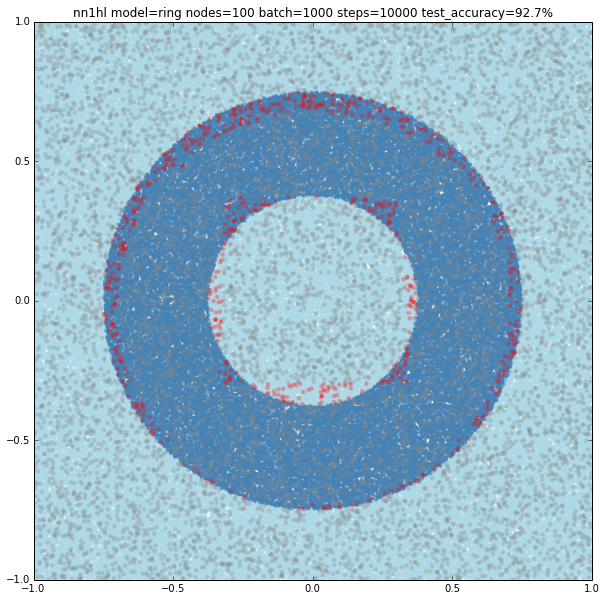
I also found that running many times with the same parameters may yield to different results. Both cases could be explained by the random initialisation and the stochastic gradient descent as the last example looks like a local minimum. Check below another interesting result using the exact same parameters yielding a pretty accurate classifier (92.7%)

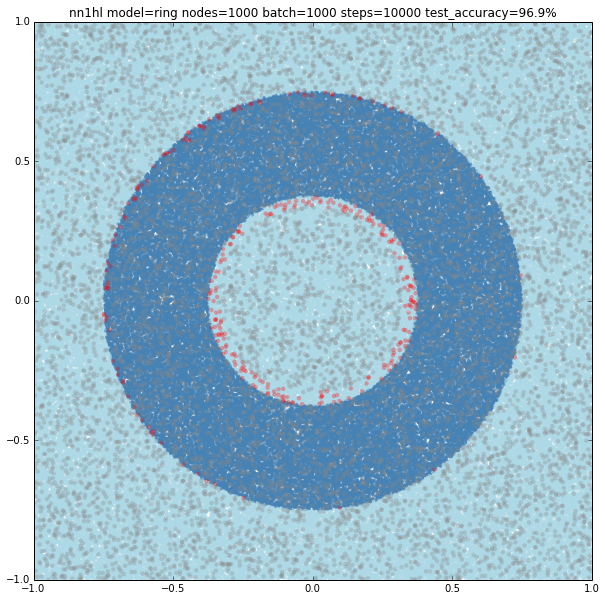
Increasing the number of nodes and the training parameters improves accuracy and makes more likely to get a classifier with a pretty good level of accuracy (96.9%). Shown below, 1000 nodes, batch size of 1000 and 10000 steps.

Cosine

With few nodes and different training parameters we see the classifier struggling to fit.

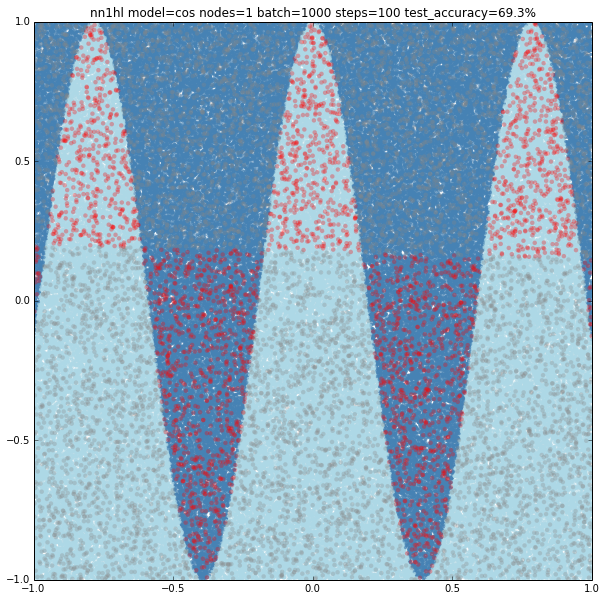
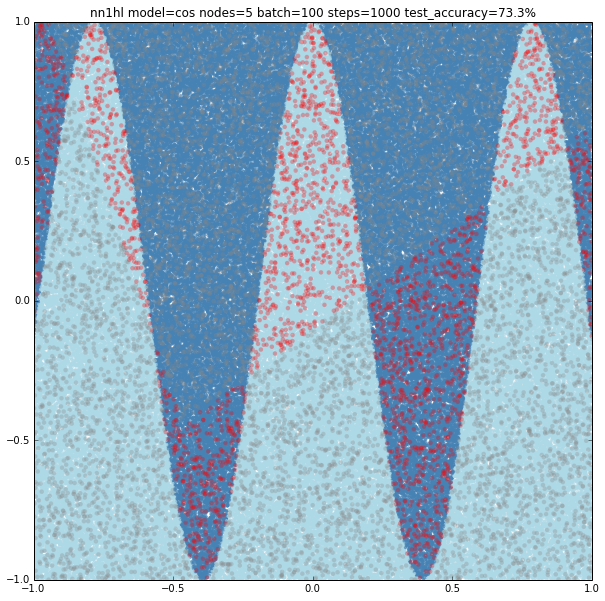
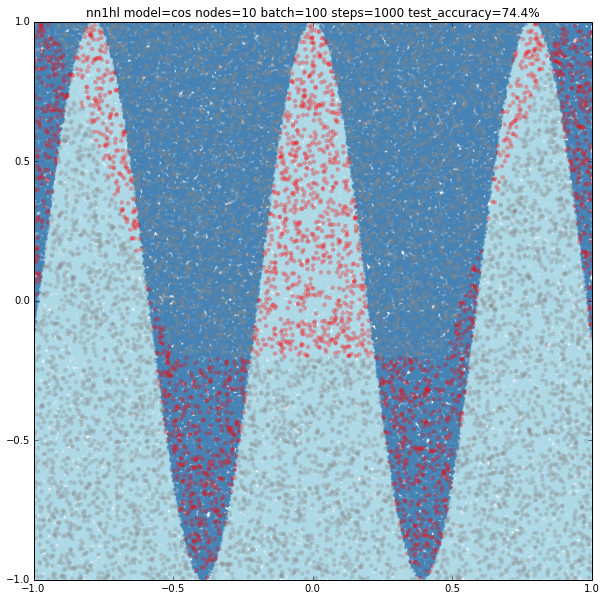
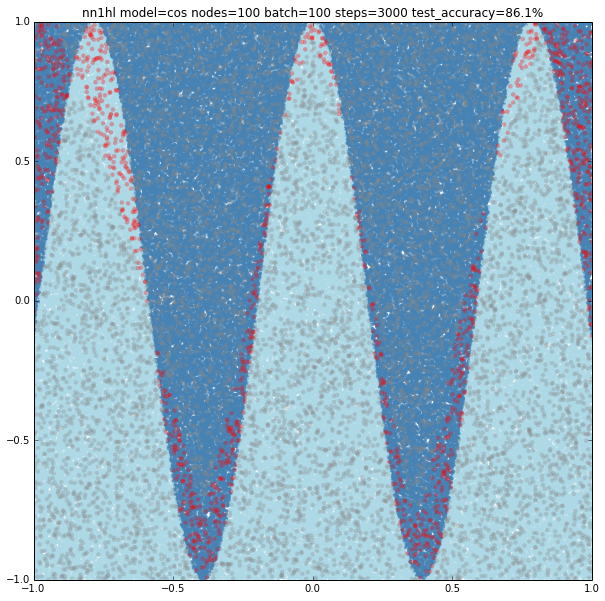
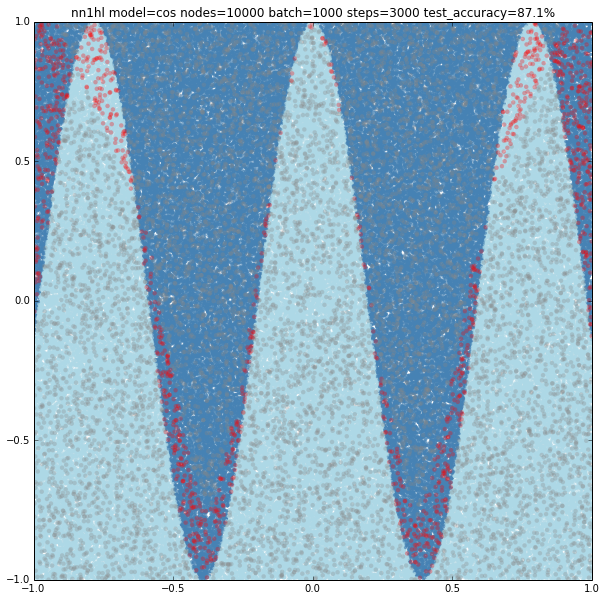
Increasing the parameters gives a model that doesn’t increase very much the accuracy (around 87%). From the ring and the cosine it looks like there are limits to the complexity a single hidden layer can handle.

Cosine in polar coordinates

This example came as a way to try a harder problem for a classifier. As expected, the most basic versions of the parameters yield bad results. Just keep in mind that a trivial classifier that labels everything as negative would have about 80% accuracy.

We can see that a NN with 10 nodes tries to adjust a central area as positive. Results are bad but we can see what the NN is trying to do. Increasing to 100 nodes give very similar results.

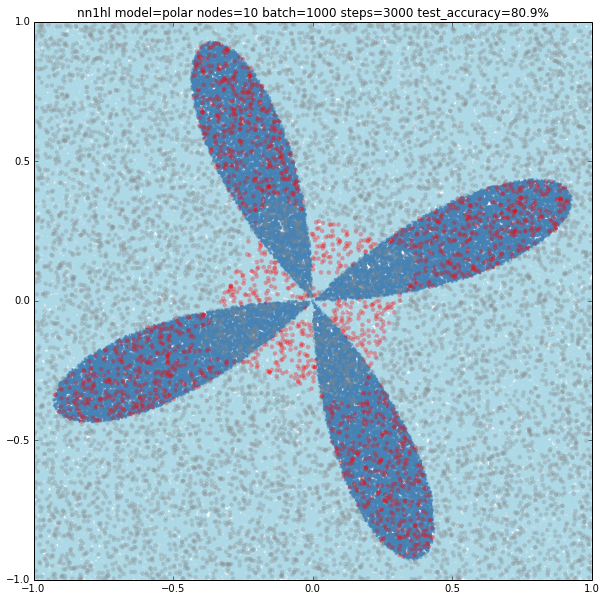
With 1000 nodes the classifier improves accuracy but misses big on the center of the model. But going up to 10,000 nodes does not improve much more. This makes me think that, as with the case of the rectangular cosine, there is a limit on what a single layer neural network may model for the classifier, and that more complex distributions may need a different kind of network.

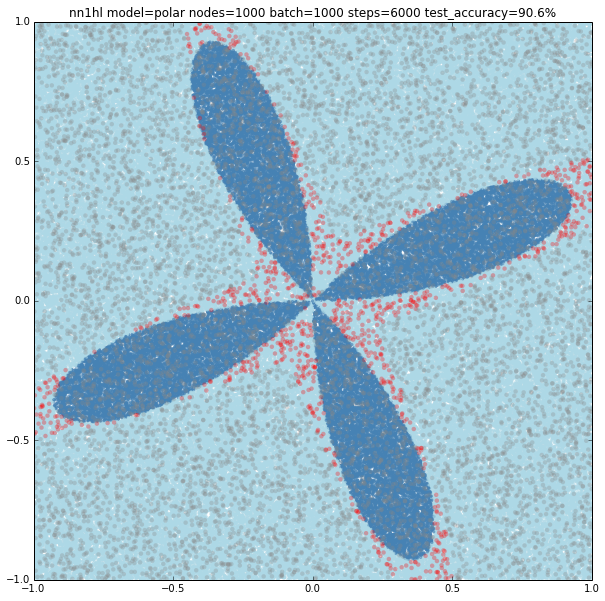
A deeper neural network

Next I was interested in what happens with deeper networks, expanding the exercises from the Udacity course to a 3 layer NN and testing with the same models.
First finding was that for the Positivos example the NN needed to be of at least 10 nodes on each layer to get good results. Same classifier also worked well for the linear model, but not with the circle.

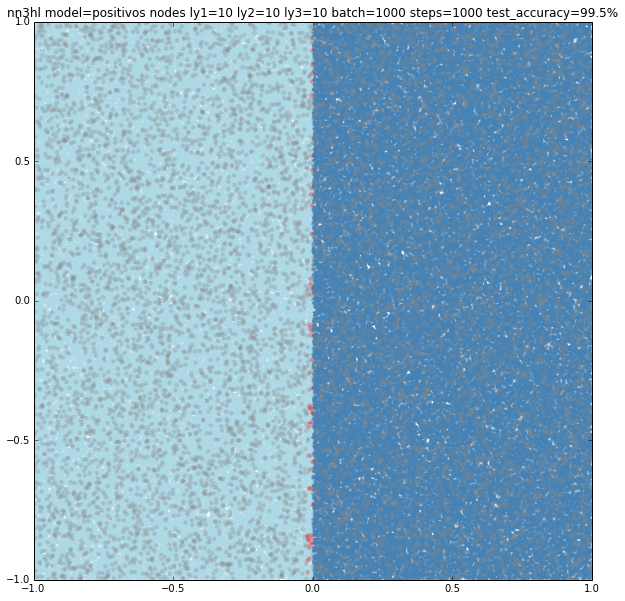
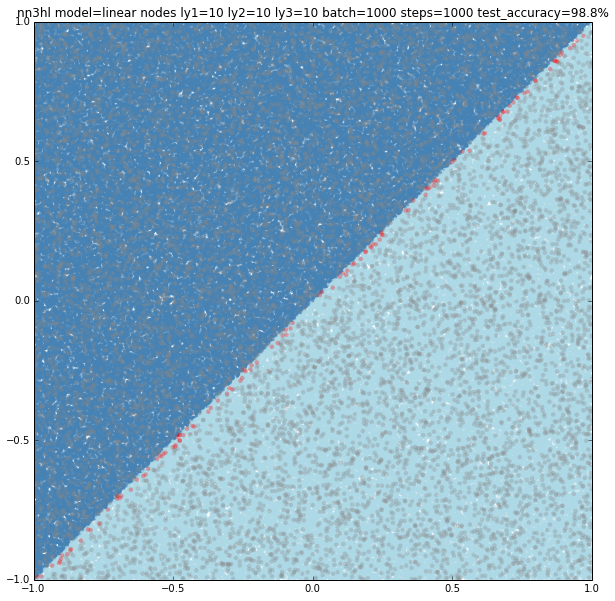
The circle needed quite an amount of nodes in some of the layers to get over 99% accuracy. The simplest model I could find with a 99.4% was (10,1000,1000) nodes. Other models with a similar count of nodes gave similar results. Models with less nodes failed completely or gave increasing accuracies.

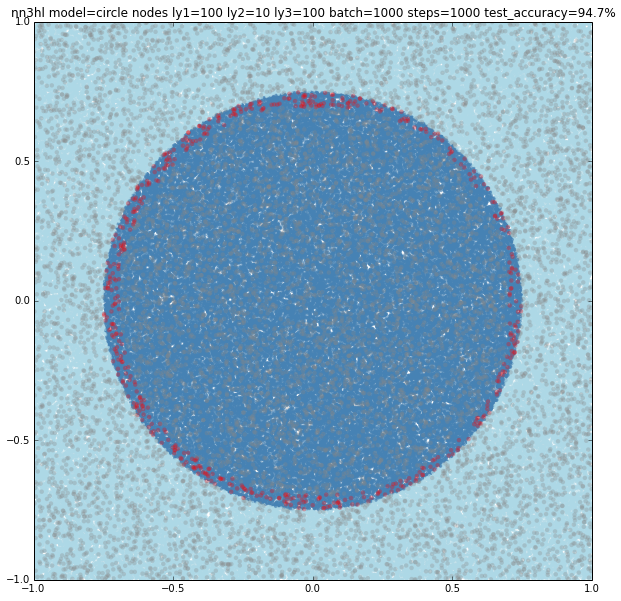
Interestingly, the ring also converged faster with (100,100,100) nodes with a 94% accuracy up to a nice 97.9% accuracy for a (1000,1000,1000) configuration.

The cosine also improved with the deeper network achieving a 94.3% accuracy with a (1000,1000,100) network. What is also interesting is that models learned by the deep network approached better than the wide network almost from the beginning. If you want to check, run the iterative version you can find commented on the code.

The Polar Cosine and Deep Network

The most interesting case is the polar cosine on the deep network as it looks like a really hard classification problem. Base accuracy is about 80.3% for the all negative classification. As we grow the number of nodes in the different layers interesting patterns appear as you can see in the examples below.

The last example does a pretty good job classifying this complex model with a 98.1% accuracy with the three layers and 1000-1000-1000 nodes.

I find very interesting seeing how the wide neural network seems to have a limit on the complexity of the classifier it can learn. And the deep network looks like being able to capture that complexity. Check the Jupyter notebook at Github. You will need Tensorflow installed to run it.